Espaces vectoriels réels ou complexes
Espaces vectoriels (et affines) :
1. Espaces vectoriels réels ou complexes
1. Espaces vectoriels réels ou complexes
Définition 1.1 : K-espace vectoriel
Soit E un ensemble, K un corps (égal en général à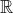 
ou 
).
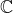On dit que (E,+,.) est un K-espace vectoriel ou espace vectoriel sur K si et seulement si :
• + est une loi de composition interne sur E : ∀ (x,y) ∈ E2, x+y existe et : x+y ∈ E,
• + est associative : ∀ (x,y,z) ∈ E3, (x + y) + z = x + (y + z),
• + possède un élément neutre dans E, en général noté 0 : ∀ x ∈ E, x + 0 = 0 + x = x,
• tout élément de E admet un symétrique pour la loi + appelé opposé de x :
∀ x ∈ E, ∃ x’ ∈ E, (x’ = -x), tel que : x + x’ = x’ + x = 0,
ce qui fait alors de (E,+) un groupe,
• + est commutative : ∀ (x,y) ∈ E2, x + y = y + x,
ce qui rend le groupe (E,+) commutatif ou abélien,
la loi . ayant de plus les propriétés suivantes :
• c’est une loi de composition externe sur E : ∀ x ∈ E, ∀ λ ∈ K, λ.x existe et : λ.x ∈ E,
• ∀ (x,y) ∈ E2, ∀ λ ∈ K, λ.(x + y) = λ.x + λ.y,
• ∀ x ∈ E, ∀ (λ,µ) ∈ K2, (λ + µ).x = λ.x + µ.x,
• ∀ x ∈ E, ∀ (λ,µ) ∈ K2, (λ.µ).x = λ.(µ.x),
• ∀ x ∈ E, 1.x = x.
Les éléments de E sont appelés « vecteurs » et ceux de K « scalaires ».
On dit que (E,+,.) est un K-espace vectoriel ou espace vectoriel sur K si et seulement si :
• + est une loi de composition interne sur E : ∀ (x,y) ∈ E2, x+y existe et : x+y ∈ E,
• + est associative : ∀ (x,y,z) ∈ E3, (x + y) + z = x + (y + z),
• + possède un élément neutre dans E, en général noté 0 : ∀ x ∈ E, x + 0 = 0 + x = x,
• tout élément de E admet un symétrique pour la loi + appelé opposé de x :
∀ x ∈ E, ∃ x’ ∈ E, (x’ = -x), tel que : x + x’ = x’ + x = 0,
ce qui fait alors de (E,+) un groupe,
• + est commutative : ∀ (x,y) ∈ E2, x + y = y + x,
ce qui rend le groupe (E,+) commutatif ou abélien,
la loi . ayant de plus les propriétés suivantes :
• c’est une loi de composition externe sur E : ∀ x ∈ E, ∀ λ ∈ K, λ.x existe et : λ.x ∈ E,
• ∀ (x,y) ∈ E2, ∀ λ ∈ K, λ.(x + y) = λ.x + λ.y,
• ∀ x ∈ E, ∀ (λ,µ) ∈ K2, (λ + µ).x = λ.x + µ.x,
• ∀ x ∈ E, ∀ (λ,µ) ∈ K2, (λ.µ).x = λ.(µ.x),
• ∀ x ∈ E, 1.x = x.
Les éléments de E sont appelés « vecteurs » et ceux de K « scalaires ».
Définition 1.2 : K-algèbre
Un ensemble (E,+,∗,.) est une K-algèbre si et seulement si :
• (E,+,.) est un K-espace vectoriel,
• ∗ est distributive par rapport à +,
• ∀ (x,y) ∈ E, ∀ λ ∈ K, λ.(x∗y) = x∗(λ.y) = (λ.x)∗y.
Si la loi ∗ est associative, commutative ou unitaire, on dit de même que l’algèbre est associative,
commutative, unitaire.
Un ensemble (E,+,∗,.) est une K-algèbre si et seulement si :
• (E,+,.) est un K-espace vectoriel,
• ∗ est distributive par rapport à +,
• ∀ (x,y) ∈ E, ∀ λ ∈ K, λ.(x∗y) = x∗(λ.y) = (λ.x)∗y.
Si la loi ∗ est associative, commutative ou unitaire, on dit de même que l’algèbre est associative,
commutative, unitaire.
Théorème 1.1 : exemples
Les ensembles suivants sont des
ou 
espaces vectoriels (suivant les cas), dits espaces vectoriels
de référence.
• les ensembles de n-uplets de réels ou de complexes :
et 
,
• les ensembles de fonctions définies sur I (éventuellement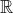), à valeurs dans 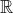, ou un K-espace
vectoriel (E,+,.) : F(I,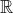), F(I,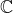) et F(I,E),
• les ensembles de polynômes à coefficients réels ou complexes :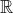[X], [X],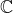 
[X] et 
[X],
• les ensembles de suites réelles ou complexes : et ,
• les ensembles de matrices carrées ou rectangles à coefficients réels ou complexes : Mn(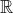), Mn(),
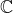Mn,p(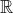), Mn,p().
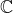Les ensembles suivants sont des K-algèbres :
• F(I,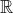), F(I,),
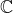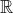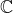•[X], [X],
• Mn(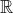), Mn().
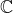Définition 1.3 : combinaison linéaire de vecteurs
Soit (E,+,.) un K-espace vectoriel.
Soit (xi)i∈I une famille (éventuellement infinie) de vecteurs de E.
Une combinaison linéaire des vecteurs de cette famille est un vecteur de E qui s’écrit :
Les ensembles suivants sont des
de référence.
• les ensembles de n-uplets de réels ou de complexes :
• les ensembles de fonctions définies sur I (éventuellement
vectoriel (E,+,.) : F(I,
• les ensembles de polynômes à coefficients réels ou complexes :
• les ensembles de suites réelles ou complexes :
• les ensembles de matrices carrées ou rectangles à coefficients réels ou complexes : Mn(
Mn,p(
Les ensembles suivants sont des K-algèbres :
• F(I,
•
• Mn(
Définition 1.3 : combinaison linéaire de vecteurs
Soit (E,+,.) un K-espace vectoriel.
Soit (xi)i∈I une famille (éventuellement infinie) de vecteurs de E.
Une combinaison linéaire des vecteurs de cette famille est un vecteur de E qui s’écrit :
où les λi sont des scalaires qui sont tous nuls, sauf au plus un nombre fini d’entre eux.
En particulier, si (xi)1≤i≤n est une famille finie de vecteurs de E, une combinaison linéaire de ces vecteurs est un vecteur de E qui s’écrit :
En particulier, si (xi)1≤i≤n est une famille finie de vecteurs de E, une combinaison linéaire de ces vecteurs est un vecteur de E qui s’écrit :
Où les λi sont n scalaires.
Théorème 1.2 : caractérisation d’un sous-espace vectoriel
Soit (E,+,.) un K-espace vectoriel et F un ensemble.
F est un sous-espace vectoriel de E si et seulement si :
• F est inclus dans E,
• F est non vide,
• F est stable par combinaison linéaire : ∀ (x,y) ∈
, ∀ (λ,µ) ∈ 
, (λ.x + µ.y) ∈ F.
Théorème 1.3 et définition 1.5 : espace vectoriel produit
Soient (E+,.) et (F,+,.) deux K-espaces vectoriels (où l’on note de la même façon dans E et F les lois de
composition internes et externes).
Alors les lois + et . définies par :
• ∀ ((x,y), (x’,y’)) ∈^2 "(E\times F)^2")
, (x,y) + (x’,y’) = (x+x’,y+y’),
• ∀ (x,y) ∈ E×F, ∀ λ ∈ K, λ.(x,y) = (λ.x,λ.y),
font de E×F un K-espace vectoriel, appelé espace vectoriel produit de E et de F.
2. Combinaisons linéaires et familles .
Définition 2.1 : famille libre de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On dit que (xi) est une famille libre si et seulement si toute combinaison linéaire nulle de ces vecteurs est
nécessairement à coefficients nuls.
En particulier, si la famille (xi) est finie de la forme (xi)1≤i≤n, la famille est libre si et seulement si :
∀ (λ1, ..., λn) ∈ Kn, (λ1.x1 + … + λn.xn = 0) ⇒ (λ1 = … = λn = 0).
Définition 2.2 : famille liée de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
La famille (xi) est dite liée si et seulement si elle n’est pas libre.
En particulier, si la famille (xi) est finie de la forme (xi)1≤i≤n, la famille est liée si et seulement si :
∃ (λ1, ..., λn) ∈ Kn, (λ1, ..., λn) ≠ (0, …,0), (λ1.x1 + … + λn.xn = 0).
Théorème 2.1 : caractérisation des familles liées
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
La famille est liée si et seulement si l’un des vecteurs de cette famille (on ne sait pas a priori lequel) peut
s’écrire comme combinaison linéaire des autres vecteurs de la famille.
Théorème 2.2 : cas où l’un des vecteurs de la famille est nul
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
Si la famille comporte le vecteur nul ou deux fois le même vecteur, la famille est liée.
Définition 2.3 : rang d’une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On appelle rang de la famille, lorsqu’il existe, le plus grand nombre de vecteurs de la famille constituant
une famille libre de vecteurs de E, et on le note rg((xi)).
Le rang d’une famille finie de n vecteurs existe donc toujours et est toujours inférieur ou égal à n.
Définition 2.4 : sous-espace vectoriel engendré par une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et A une famille de vecteurs de E.
On appelle sous-espace vectoriel de E engendré par la famille A l’ensemble noté Vect(A) des
combinaisons linéaires de vecteurs de A, soit :
Vect(A) = {x ∈ E, ∃ (x1, …, xp) ∈ Ap, ∃ (λ1, …,λp) ∈ Kp, x = λ1.x1 + … + λp.xp}.
En particulier, si : A = (xi)1≤i≤n, on a : Vect(A) = {x ∈ E, ∃ (λ1, …,λn) ∈ Kn, x = λ1.x1 + … + λp.xp}.
Théorème 2.3 : caractérisation d’un sous-espace vectoriel engendré
Soit (E,+,.) un K-espace vectoriel et A un sous-ensemble de E.
Vect(A) est le plus petit sous-espace vectoriel de E contenant A, c’est-à-dire :
∀ G, sous-espace vectoriel de E, (A ⊂ G) ⇒ (Vect(A) ⊂ G)
Définition 2.5 : base d’un K-espace vectoriel
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On dit que (xi) est une base de E si et seulement si c’est une famille libre et génératrice de E.
3. Espaces vectoriels de dimension finie .
Définition 3.1 : espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel.
On dit que E est de dimension finie sur K si et seulement si E admet une famille génératrice finie.
Théorème 3.1 : de l’échange
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Soient : B = (e1, …, ep), une famille libre d’éléments de E, et : B’0 = (e’1, …, e’q), une famille génératrice
de E.
Alors : p ≤ q.
De plus, on peut échanger p des vecteurs de la famille B’0 avec les p vecteurs de la famille B pour
obtenir une nouvelle famille génératrice de E.
Théorème 3.2 : existence de bases dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Alors E admet une base comportant un nombre fini de vecteurs, et toutes les bases de E comportent le
même nombre fini de vecteurs.
Définition 3.2 : dimension d’un K-espace vectoriel
Soit (E,+,.) un K-espace vectoriel.
Si E admet une base comportant un nombre fini de vecteurs, on appelle dimension de E le nombre de
vecteurs de cette base qui est donc le même pour toutes les bases de E.
Théorème 3.3 : cardinal des familles libres ou génératrices dans un espace vectoriel de dimension
finie
Soit (E,+,.) un K-espace vectoriel de dimension finie n et (xi)1≤i≤p une famille de vecteurs de E.
Si la famille (xi)1≤i≤p est génératrice de E, alors : p ≥ n.
Si la famille (xi)1≤i≤p est libre, alors : p ≤ n.
On a les équivalences :
((xi)1≤i≤p base de E) ⇔ ((xi)1≤i≤p libre et : p = n) ⇔ ((xi)1≤i≤p génératrice de E et : p = n).
Théorème 3.4 : de la base incomplète
Soit (E,+,.) un K-espace vectoriel de dimension finie n et : B = (e1, …, en), une base de E.
Si (x1, …, xp) est une famille libre de vecteurs de E, alors il est possible de compléter la famille (x1, …, xp)
à l’aide de vecteurs de B en une nouvelle base de E.
Théorème 3.5 : dimension d’un sous-espace vectoriel dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Tout sous-espace vectoriel de E est de dimension finie, inférieure à celle de E.
Théorème 3.6 : caractérisation du rang d’une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi)1≤i≤p une famille finie de vecteurs de E.
Alors le rang de la famille (xi)1≤i≤p est égal à la dimension du sous-espace vectoriel de E engendré par
cette famille.
Soit donc : rg(x1, …, xp) = dim(Vect(x1, …, xp)).
Théorème 3.7 : égalité de sous-espaces vectoriels dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel.
Soient F et G des sous-espaces vectoriels de dimension finie de E.
Alors : (F = G) ⇔ (F ⊂ G, et : dim(F) = dim(G)).
En particulier, si E est lui-même de dimension finie, pour tout sous-espace vectoriel F de E, on a :
(E = F) ⇔ (dim(F) = dim(E)).
4. Applications linéaires
Définition 4.1 : application linéaire entre K-espaces vectoriels, L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
On dit que u est une application de E dans F est linéaire si et seulement si :
∀ (x,y) ∈ E2, ∀ (λ,µ) ∈ K2, u(λ.x + µ.y) = λ.u(x) + µ.u(y).
L’ensemble des applications linéaires de E dans F est noté L(E,F), et on note : L(E,E) = L(E).
Théorème 4.1 : structure de K-espace vectoriel de L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
L(E,F) peut être muni d’une structure de K-espace vectoriel et L(E) d’une structure de K-algèbre.
Définition 4.2 : le groupe linéaire d’un espace vectoriel
Soit (E,+,.) un K-espace vectoriel.
L’ensemble des automorphismes de E forme un groupe pour la composition des applications, appelé
groupe linéaire de E et noté Gl(E).
Définition 4.3 : morphisme, endomorphisme, isomorphisme, automorphisme
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
Une application linéaire de E dans F est appelée morphisme ou homomorphisme de E dans F.
Un endomorphisme de E est une application linéaire de E dans lui-même.
Un isomorphisme de E dans F est une application linéaire bijective de E dans F.
Un automorphisme de E est une application linéaire bijective de E dans lui-même.
Définition 4.4 : image et noyau d’une application linéaire
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, et : u ∈ L(E,F).
On appelle image de u et noyau de u les ensembles :
• Im(u) = {y ∈ F, ∃ x ∈ E, y = u(x)},
• ker(u) = {x ∈ E, u(x) = 0}.
Théorème 4.2 : image et noyau d’un morphisme sont des sous-espaces vectoriels
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, et : u ∈ L(E,F).
Alors Im(u) est un sous-espace vectoriel de F et ker(u) un sous-espace vectoriel de E.
Théorème 4.3 : caractérisation de l’injectivité et de la surjectivité
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels et : u ∈ L(E,F).
Alors :
• (u injective) ⇔ (ker(u) = {0}).
• (u surjective) ⇔ (Im(u) = F).
Théorème 4.4 : caractérisation d’une application linéaire par son action sur une somme directe
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
Soient E1, …, En, des sous-espaces vectoriels de E tels que : E =
, et (ui)1≤i≤n une famille telle que :
∀ 1 ≤ i ≤ n, ui ∈ L(Ei,F).
Alors il existe une unique application linéaire : u ∈ L(E,F), telle que : ∀ 1 ≤ i ≤ n, u i = u Ei .
Théorème 4.5 : isomorphisme entre l’image d’un morphisme et un supplémentaire de son noyau
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels et : u ∈ L(E,F).
Soit E’ un supplémentaire de ker(u) dans E.
Alors u permet de définir un isomorphisme de E’ sur Im(u).
5. Applications linéaires en dimension finie .
Théorème 5.1 : famille génératrice de l’image d’un morphisme en dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie et : u ∈ L(E,F).
Soit : B = (e1, …, en), une famille génératrice de E.
Alors (u(e1), …, u(en)) est une famille génératrice de Im(u).
En particulier, Im(u) est un sous-espace vectoriel de F de dimension finie, inférieure à celle de E.
Théorème 5.2 : caractérisation d’une application linéaire par les images des vecteurs d’une base
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie n.
Soit : B = (e1, …, en), une base de E, et (a1, …, an) une famille de vecteurs de F.
Alors : ∃ ! u ∈ L(E,F), ∀ 1 ≤ i ≤ n, u(ei) = ai.
Autrement dit, une application linéaire de E dans F est entièrement définie par la donnée des images
des vecteurs d’une base de l’espace de départ E.
Définition 5.1 : rang d’une application linéaire en dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie, et : u ∈ L(E,F).
On appelle rang de u la dimension de Im(u) : rg(u) = dim(Im(u)).
Théorème 5.3 : du rang
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie et : u ∈ L(E,F).
Alors : dim(Im(u)) + dim(ker(u)) = dim(E).
Théorème 5.4 : caractérisation des isomorphismes entre espaces de dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie, u ∈ L(E,F).
Il y a équivalence entre les propositions suivantes :
• u est un isomorphisme de E sur F,
• u est injective et : dim(E) = dim(F),
• u est surjective et : dim(E) = dim(F).
En particulier, pour : u ∈ L(E), toujours avec E de dimension finie, on a les équivalences :
(u bijective) ⇔ (u injective) ⇔ (u surjective).
Théorème 5.5 : conservation du rang par isomorphisme
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie, u un isomorphisme de E sur F.
Soit (x1, … ,xn) une famille de vecteurs de E.
Alors : rg(x1, … ,xn) = rg(u(x1), … , u(xn)).
Théorème 5.6 : dimension de L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie.
Alors L(E,F) est de dimension finie et : dim(L(E,F)) = dim(E).dim(F).
En particulier, toujours si E est de dimension finie, L(E) a pour dimension (dim(E))2.
Espaces vectoriels réels ou complexes:
Soit (E,+,.) un K-espace vectoriel et F un ensemble.
F est un sous-espace vectoriel de E si et seulement si :
• F est inclus dans E,
• F est non vide,
• F est stable par combinaison linéaire : ∀ (x,y) ∈
Théorème 1.3 et définition 1.5 : espace vectoriel produit
Soient (E+,.) et (F,+,.) deux K-espaces vectoriels (où l’on note de la même façon dans E et F les lois de
composition internes et externes).
Alors les lois + et . définies par :
• ∀ ((x,y), (x’,y’)) ∈
• ∀ (x,y) ∈ E×F, ∀ λ ∈ K, λ.(x,y) = (λ.x,λ.y),
font de E×F un K-espace vectoriel, appelé espace vectoriel produit de E et de F.
2. Combinaisons linéaires et familles .
Définition 2.1 : famille libre de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On dit que (xi) est une famille libre si et seulement si toute combinaison linéaire nulle de ces vecteurs est
nécessairement à coefficients nuls.
En particulier, si la famille (xi) est finie de la forme (xi)1≤i≤n, la famille est libre si et seulement si :
∀ (λ1, ..., λn) ∈ Kn, (λ1.x1 + … + λn.xn = 0) ⇒ (λ1 = … = λn = 0).
Définition 2.2 : famille liée de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
La famille (xi) est dite liée si et seulement si elle n’est pas libre.
En particulier, si la famille (xi) est finie de la forme (xi)1≤i≤n, la famille est liée si et seulement si :
∃ (λ1, ..., λn) ∈ Kn, (λ1, ..., λn) ≠ (0, …,0), (λ1.x1 + … + λn.xn = 0).
Théorème 2.1 : caractérisation des familles liées
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
La famille est liée si et seulement si l’un des vecteurs de cette famille (on ne sait pas a priori lequel) peut
s’écrire comme combinaison linéaire des autres vecteurs de la famille.
Théorème 2.2 : cas où l’un des vecteurs de la famille est nul
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
Si la famille comporte le vecteur nul ou deux fois le même vecteur, la famille est liée.
Définition 2.3 : rang d’une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On appelle rang de la famille, lorsqu’il existe, le plus grand nombre de vecteurs de la famille constituant
une famille libre de vecteurs de E, et on le note rg((xi)).
Le rang d’une famille finie de n vecteurs existe donc toujours et est toujours inférieur ou égal à n.
Définition 2.4 : sous-espace vectoriel engendré par une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et A une famille de vecteurs de E.
On appelle sous-espace vectoriel de E engendré par la famille A l’ensemble noté Vect(A) des
combinaisons linéaires de vecteurs de A, soit :
Vect(A) = {x ∈ E, ∃ (x1, …, xp) ∈ Ap, ∃ (λ1, …,λp) ∈ Kp, x = λ1.x1 + … + λp.xp}.
En particulier, si : A = (xi)1≤i≤n, on a : Vect(A) = {x ∈ E, ∃ (λ1, …,λn) ∈ Kn, x = λ1.x1 + … + λp.xp}.
Théorème 2.3 : caractérisation d’un sous-espace vectoriel engendré
Soit (E,+,.) un K-espace vectoriel et A un sous-ensemble de E.
Vect(A) est le plus petit sous-espace vectoriel de E contenant A, c’est-à-dire :
∀ G, sous-espace vectoriel de E, (A ⊂ G) ⇒ (Vect(A) ⊂ G)
Définition 2.5 : base d’un K-espace vectoriel
Soit (E,+,.) un K-espace vectoriel et (xi) une famille de vecteurs de E.
On dit que (xi) est une base de E si et seulement si c’est une famille libre et génératrice de E.
3. Espaces vectoriels de dimension finie .
Définition 3.1 : espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel.
On dit que E est de dimension finie sur K si et seulement si E admet une famille génératrice finie.
Théorème 3.1 : de l’échange
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Soient : B = (e1, …, ep), une famille libre d’éléments de E, et : B’0 = (e’1, …, e’q), une famille génératrice
de E.
Alors : p ≤ q.
De plus, on peut échanger p des vecteurs de la famille B’0 avec les p vecteurs de la famille B pour
obtenir une nouvelle famille génératrice de E.
Théorème 3.2 : existence de bases dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Alors E admet une base comportant un nombre fini de vecteurs, et toutes les bases de E comportent le
même nombre fini de vecteurs.
Définition 3.2 : dimension d’un K-espace vectoriel
Soit (E,+,.) un K-espace vectoriel.
Si E admet une base comportant un nombre fini de vecteurs, on appelle dimension de E le nombre de
vecteurs de cette base qui est donc le même pour toutes les bases de E.
Théorème 3.3 : cardinal des familles libres ou génératrices dans un espace vectoriel de dimension
finie
Soit (E,+,.) un K-espace vectoriel de dimension finie n et (xi)1≤i≤p une famille de vecteurs de E.
Si la famille (xi)1≤i≤p est génératrice de E, alors : p ≥ n.
Si la famille (xi)1≤i≤p est libre, alors : p ≤ n.
On a les équivalences :
((xi)1≤i≤p base de E) ⇔ ((xi)1≤i≤p libre et : p = n) ⇔ ((xi)1≤i≤p génératrice de E et : p = n).
Théorème 3.4 : de la base incomplète
Soit (E,+,.) un K-espace vectoriel de dimension finie n et : B = (e1, …, en), une base de E.
Si (x1, …, xp) est une famille libre de vecteurs de E, alors il est possible de compléter la famille (x1, …, xp)
à l’aide de vecteurs de B en une nouvelle base de E.
Théorème 3.5 : dimension d’un sous-espace vectoriel dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel de dimension finie.
Tout sous-espace vectoriel de E est de dimension finie, inférieure à celle de E.
Théorème 3.6 : caractérisation du rang d’une famille de vecteurs
Soit (E,+,.) un K-espace vectoriel et (xi)1≤i≤p une famille finie de vecteurs de E.
Alors le rang de la famille (xi)1≤i≤p est égal à la dimension du sous-espace vectoriel de E engendré par
cette famille.
Soit donc : rg(x1, …, xp) = dim(Vect(x1, …, xp)).
Théorème 3.7 : égalité de sous-espaces vectoriels dans un espace vectoriel de dimension finie
Soit (E,+,.) un K-espace vectoriel.
Soient F et G des sous-espaces vectoriels de dimension finie de E.
Alors : (F = G) ⇔ (F ⊂ G, et : dim(F) = dim(G)).
En particulier, si E est lui-même de dimension finie, pour tout sous-espace vectoriel F de E, on a :
(E = F) ⇔ (dim(F) = dim(E)).
4. Applications linéaires
Définition 4.1 : application linéaire entre K-espaces vectoriels, L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
On dit que u est une application de E dans F est linéaire si et seulement si :
∀ (x,y) ∈ E2, ∀ (λ,µ) ∈ K2, u(λ.x + µ.y) = λ.u(x) + µ.u(y).
L’ensemble des applications linéaires de E dans F est noté L(E,F), et on note : L(E,E) = L(E).
Théorème 4.1 : structure de K-espace vectoriel de L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
L(E,F) peut être muni d’une structure de K-espace vectoriel et L(E) d’une structure de K-algèbre.
Définition 4.2 : le groupe linéaire d’un espace vectoriel
Soit (E,+,.) un K-espace vectoriel.
L’ensemble des automorphismes de E forme un groupe pour la composition des applications, appelé
groupe linéaire de E et noté Gl(E).
Définition 4.3 : morphisme, endomorphisme, isomorphisme, automorphisme
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
Une application linéaire de E dans F est appelée morphisme ou homomorphisme de E dans F.
Un endomorphisme de E est une application linéaire de E dans lui-même.
Un isomorphisme de E dans F est une application linéaire bijective de E dans F.
Un automorphisme de E est une application linéaire bijective de E dans lui-même.
Définition 4.4 : image et noyau d’une application linéaire
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, et : u ∈ L(E,F).
On appelle image de u et noyau de u les ensembles :
• Im(u) = {y ∈ F, ∃ x ∈ E, y = u(x)},
• ker(u) = {x ∈ E, u(x) = 0}.
Théorème 4.2 : image et noyau d’un morphisme sont des sous-espaces vectoriels
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, et : u ∈ L(E,F).
Alors Im(u) est un sous-espace vectoriel de F et ker(u) un sous-espace vectoriel de E.
Théorème 4.3 : caractérisation de l’injectivité et de la surjectivité
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels et : u ∈ L(E,F).
Alors :
• (u injective) ⇔ (ker(u) = {0}).
• (u surjective) ⇔ (Im(u) = F).
Théorème 4.4 : caractérisation d’une application linéaire par son action sur une somme directe
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels.
Soient E1, …, En, des sous-espaces vectoriels de E tels que : E =
∀ 1 ≤ i ≤ n, ui ∈ L(Ei,F).
Alors il existe une unique application linéaire : u ∈ L(E,F), telle que : ∀ 1 ≤ i ≤ n, u i = u Ei .
Théorème 4.5 : isomorphisme entre l’image d’un morphisme et un supplémentaire de son noyau
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels et : u ∈ L(E,F).
Soit E’ un supplémentaire de ker(u) dans E.
Alors u permet de définir un isomorphisme de E’ sur Im(u).
5. Applications linéaires en dimension finie .
Théorème 5.1 : famille génératrice de l’image d’un morphisme en dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie et : u ∈ L(E,F).
Soit : B = (e1, …, en), une famille génératrice de E.
Alors (u(e1), …, u(en)) est une famille génératrice de Im(u).
En particulier, Im(u) est un sous-espace vectoriel de F de dimension finie, inférieure à celle de E.
Théorème 5.2 : caractérisation d’une application linéaire par les images des vecteurs d’une base
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie n.
Soit : B = (e1, …, en), une base de E, et (a1, …, an) une famille de vecteurs de F.
Alors : ∃ ! u ∈ L(E,F), ∀ 1 ≤ i ≤ n, u(ei) = ai.
Autrement dit, une application linéaire de E dans F est entièrement définie par la donnée des images
des vecteurs d’une base de l’espace de départ E.
Définition 5.1 : rang d’une application linéaire en dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie, et : u ∈ L(E,F).
On appelle rang de u la dimension de Im(u) : rg(u) = dim(Im(u)).
Théorème 5.3 : du rang
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels, E de dimension finie et : u ∈ L(E,F).
Alors : dim(Im(u)) + dim(ker(u)) = dim(E).
Théorème 5.4 : caractérisation des isomorphismes entre espaces de dimension finie
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie, u ∈ L(E,F).
Il y a équivalence entre les propositions suivantes :
• u est un isomorphisme de E sur F,
• u est injective et : dim(E) = dim(F),
• u est surjective et : dim(E) = dim(F).
En particulier, pour : u ∈ L(E), toujours avec E de dimension finie, on a les équivalences :
(u bijective) ⇔ (u injective) ⇔ (u surjective).
Théorème 5.5 : conservation du rang par isomorphisme
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie, u un isomorphisme de E sur F.
Soit (x1, … ,xn) une famille de vecteurs de E.
Alors : rg(x1, … ,xn) = rg(u(x1), … , u(xn)).
Théorème 5.6 : dimension de L(E,F)
Soient (E,+,.) et (F,+,.) des K-espaces vectoriels de dimension finie.
Alors L(E,F) est de dimension finie et : dim(L(E,F)) = dim(E).dim(F).
En particulier, toujours si E est de dimension finie, L(E) a pour dimension (dim(E))2.
Espaces vectoriels réels ou complexes:
- K-espace vectoriel
- K-algèbre
- combinaison linéaire de vecteurs
- sous-espace vectoriel d’un espace vectoriel
- caractérisation d’un sous-espace vectoriel
- espace vectoriel produit
- famille libre de vecteurs
- famille liée de vecteurs
- caractérisation des familles liées
- rang d’une famille de vecteurs
- sous-espace vectoriel engendré par une famille de vecteurs
- caractérisation d’un sous-espace vectoriel engendré
- base d’un K-espace vectoriel
- espace vectoriel de dimension finie
- existence de bases dans un espace vectoriel de dimension finie
- dimension d’un K-espace vectoriel
- cardinal des familles libres ou génératrices dans un espace vectoriel de dimension finie
- dimension d’un sous-espace vectoriel dans un espace vectoriel de dimension finie
- caractérisation du rang d’une famille de vecteurs
- égalité de sous-espaces vectoriels dans un espace vectoriel de dimension finie
- application linéaire entre K-espaces vectoriels, L(E,F)
- structure de K-espace vectoriel de L(E,F)
- le groupe linéaire d’un espace vectoriel
- morphisme, endomorphisme, isomorphisme, automorphisme
- image et noyau d’une application linéaire
- image et noyau d’un morphisme sont des sous-espaces vectoriels
- caractérisation de l’injectivité et de la surjectivité
- caractérisation d’une application linéaire par son action sur une somme directe
- isomorphisme entre l’image d’un morphisme et un supplémentaire de son noyau
- famille génératrice de l’image d’un morphisme en dimension finie
- caractérisation d’une application linéaire par les images des vecteurs d’une base
- rang d’une application linéaire en dimension finie
- caractérisation des isomorphismes entre espaces de dimension finie
- conservation du rang par isomorphisme
- dimension de L(E,F)
- les espaces vectoriels de matrices
- produit de matrices
- structure de groupe et d’algèbre pour Mn(K)
- matrice transposée d’une matrice
- matrice symétrique, antisymétrique
- dimension et supplémentarité de Sn(K) et An(K)
- Espaces vectoriels (et affines) – Cours complet. - 2 -
- matrice définie par blocs
- matrices triangulaires ou diagonales par blocs
- somme et produit de matrices par blocs
- matrice des coordonnées d’un vecteur dans une base
- matrice de changement de base (matrice de passage)
- lien entre les coordonnées d’un même vecteur dans différentes bases
- matrice représentative d’une application linéaire dans des bases
- isomorphisme entre Mn,p(K) et L(E,F)
- traduction matricielle du lien entre un vecteur et son image par un morphisme
- application linéaire ou endomorphisme canoniquement associé à une matrice
- matrice d’une composée
- liens entre les matrices de passage pour trois bases de l’espace
- lien entre les matrices d’un même endomorphisme dans différentes bases
- somme de sous-espaces vectoriels
- autre définition d’une somme de sous-espaces vectoriels
- somme directe de deux ou de plusieurs sous-espaces vectoriels
- sous-espaces supplémentaires
- existence d’un supplémentaire en dimension finie
- des quatre dimensions ou formule de Grassmann
- décomposition en somme directe
- propriété récursive des sommes directes
- définition équivalente d’une décomposition en somme directe
- caractérisation d’une décomposition en somme directe
- base d’un espace vectoriel adaptée à un sous-espace vectoriel, à une somme directede sous-espaces vectoriels
- projecteurs associés à deux sous-espaces vectoriels supplémentaires
- propriétés pour des projecteurs associés
- caractérisation des sous-espaces vectoriels définissant un projecteur
- famille de projecteurs associée à une décomposition en somme directe
- généralisation du théorème 10.1
- polynômes de Lagrange
- existence et unicité des bases de Lagrange
- trace d’une matrice carrée
- propriétés basiques de la trace des matrices
- trace d’un endomorphisme
- trace d’un projecteur
- dual d’un espace
- dimension du dual pour un espace de dimension finie
- hyperplan (en dimension finie)
- noyau des formes linéaires non nulles
- base duale d’une base en dimension finie
- base préduale (ou anté-duale) d’une base de E*
- équations d’un hyperplan
- espace affine
- Espaces vectoriels (et affines) – Cours complet. - 3 -
- structure affine de 2 et 3
- propriétés élémentaires liant des vecteurs dans un espace affine
- repère affine ou cartésien
- coordonnées d’un point dans un repère
- sous-espace affine
- sous-espaces affines de 2 et 3
- sous-espaces affines parallèles
- représentation paramétrique de droites et de plans dans un repère de 2 ou de 3
- équation d’une droite dans un repère de 2 ou d’un plan dans un repère de 3
- application affine
- expression d’une application affine dans un repère de 2 ou de 3
- exemples d’applications affines
- barycentre de n points pondérés
- coordonnées du barycentre de n points dans un repère
- associativité du barycentre
ليست هناك تعليقات